Le Nombre d’or est girardien

par Jean-Louis Salasc

Petite rêverie mathématico-mimétique…

Le Nombre d’or est une curiosité mathématique. Euclide fut le premier à en parler : c’est la proportion qui divise un segment en deux sous-segments inégaux, de telle sorte que le rapport du petit au grand est le même que celui du grand au tout.

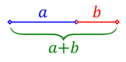
Avec donc la proportion :

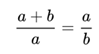
Cette proportion est le Nombre d’or, dénommé φ (Phi) en hommage au sculpteur de l’antiquité grecque, Phidias. Comme chacun sait, sa valeur est de 1,61803398875… le nombre de décimales étant infini. On en reste en général à 1,618 et à 61,8% sous forme de pourcentage.

Ce nombre possède de nombreuses particularités intrigantes, qu’il serait fastidieux d’énumérer ici ; Internet regorge de sites qui en font des présentations plus ou moins spectaculaires. Néanmoins, d’un strict point de vue mathématique, φ  n’est pas d’une immense utilité. Il se trouve certes dans diverses constructions géométriques (pentagones, spirales, triangles, etc.) mais son prestige lui vient de considérations bien différentes.

Parmi l’infinité de rectangles que vous pouvez dessiner, se trouve celui dit « Rectangle d’or » ; ainsi nommé parce que la proportion entre son grand côté et son petit côté est celle du Nombre d’or. Un petit croquis vaut mieux qu’un long discours :

Eh bien depuis la Grèce antique, ce rectangle a la réputation d’être le plus harmonieux d’entre tous. Nous glissons de l’objectivité mathématique vers un jugement esthétique. D’où cela vient-il ?

Nous serions tentés de suggérer un nom, encore que le phénomène s’apparente sans doute davantage au consensus d’une époque. Ce nom est celui d’Aristote, selon qui l’art se doit d’imiter la nature.

Et en effet, la proportion du Nombre d’or est très présente dans la nature. Divers coquillages suivent la spirale qu’il engendre, de même que les fougères ; il règle les figures de la peau d’ananas, de la fleur de tournesol, des pommes de pin ; il se retrouve dans plusieurs fleurs, plantes et arbres. Il est même possible de dire que vous-mêmes, chers lecteurs, l’avez en main puisque vos différentes phalanges en donnent successivement la proportion approximative.

Le culte du Nombre prend son essor à la Renaissance. Luca Pacioli, un moine et géomètre, lui consacre un traité intitulé « La Divine Proportion », pour lequel son ami Léonard de Vinci dessine des illustrations, en particulier le célèbre « Homme de Vitruve ».

 Et dès lors les spécialistes s’acharnent à débusquer la présence de φ dans les Pyramides, le Parthénon, la cathédrale de Chartres, La Joconde, les tableaux de Poussin, etc.  Le Nombre d’or devient un canon esthétique, un secret pour parvenir au Beau, presque une mystique.

La survenue des Lumières puis des très rationalistes XIXème et XXème siècles allait-elle « déconstruire » le mythe du Nombre d’or ?

Pas le moins du monde.

Vers 1780, Haydn et Mozart mettent au point l’une des formes majeures de la musique, la forme-sonate ; son moment stratégique en est le retour de la mélodie principale dans la tonalité d’origine. Chez nos deux musiciens, ce moment survient très généralement aux  deux-tiers du morceau, c’est-à-dire approximativement à la proportion du Nombre d’or.

Etait-ce voulu ? Le débat reste ouvert. Mais deux siècles plus tard, un Bartok ou un Xenakis revendiquent sciemment et consciemment l’usage du Nombre d’or pour élaborer leurs morceaux. Pendant ce temps, Gaudi s’en inspire pour les pavages de la Sagrada Familia. Le Corbusier travaille avec le Modulor, un outil de son invention intégrant le Nombre d’or et les proportions du corps humain. Nos amis photographes emploient couramment la règle des tiers, qui en dérive. Et Photoshop, fleuron des Nouvelles Technologies de l’Information, en recommande activement l’usage. Les colonels Wang Xiangsui et Qiao Liang, rénovateurs de la pensée stratégique et militaire chinoise avec leur ouvrage « La Guerre hors limite » (1999), font du Nombre d’or un repère fondamental de leur domaine (et se gaussent au passage de l’Occident, qui, selon eux, en aurait oublié le secret).

Et pourtant, cette idolâtrie ne résiste pas vingt secondes aux constats les plus élémentaires. En effet beaucoup de phénomènes naturels sont régis par des chiffres, des proportions ou des lois sans le moindre rapport avec notre malheureux φ. D’innombrables chefs d’œuvres, dans tous les domaines, n’ont aucun lien avec lui.

Ainsi donc, le Nombre d’or, divinisé jusque dans le temps des « déconstructions » radicales et systématiques, devrait-il être « rejeté comme la pierre de faîte » ?

En bien non, il peut rester une référence : et cela, grâce à la théorie mimétique (si ce billet devait devenir un clip vidéo, il serait séant d’introduire ici un vigoureux roulement de tambour pour souligner la solennité du moment). Il s’agit bien sûr de conserver φ comme référence rationnelle et non de faire perdurer le caractère magico-religieux qui lui est encore attribué.

Expliquons-nous.

Le girardien du rang sait à quel point le mimétisme est ambivalent. Son versant lumineux est celui de l’admiration, de l’apprentissage et de l’émulation ; sa face sombre est celle de l’envie, de la rivalité et de la violence. Comment faire face cette ambivalence, à défaut de la maîtriser ?

Une fois de plus, c’est René Girard qui nous met sur la piste. La rivalité, nous dit-il, jaillit d’une trop grande proximité, d’une trop grande similitude ; le matelot se voit comme rival du quartier-maître, pas du contre-amiral.

A l’opposé, un éloignement maximal est tout simplement le signe de l’absence de mimétisme : aucun risque de violence en effet, mais tout le versant lumineux du mimétisme est perdu.

Ainsi donc, l’ambivalence du mimétisme s’appréhende-t-elle comme une dialectique de l’éloignement et de la proximité, du distinct et du semblable. Existerait-il un point d’équilibre, un compromis entre les deux termes ?

C’est ici que nous pouvons proposer notre ami le Nombre d’or.

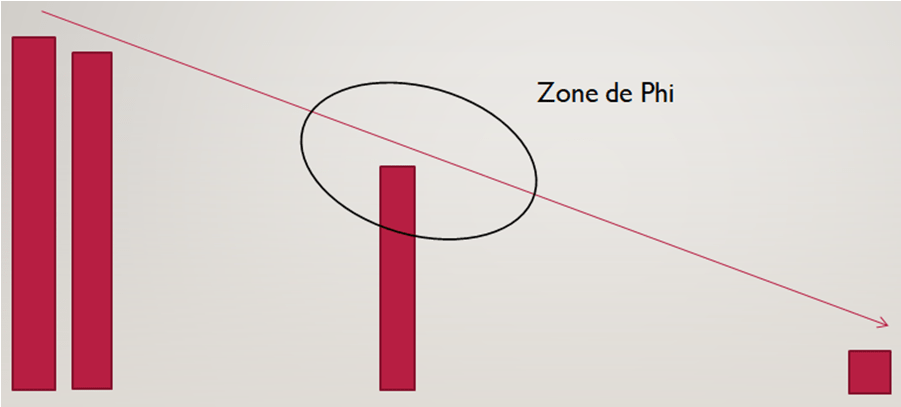
Il représente un optimum entre différence et identité ; avec une proportion plus élevée, nous nous approchons dangereusement de la zone de rivalité ; avec une proportion plus faible, nous perdons les bienfaits du mimétisme. φ représente la manière la plus dissemblable d’être identiques, qui est aussi la manière la plus similaire d’être différents.

Mais dans toute bonne histoire girardienne, il nous faut un rival. Et le Nombre d’or en a un : c’est le partage 50/50 ; la moitié ; 0,5 au lieu de 0,618. Et il est vrai que ce partage en deux est des plus présents dans la nature et dans les créations humaines.

Je vous propose néanmoins de le rejeter fermement et de donner la palme au Nombre d’or.

Pourquoi ? Pour deux raisons. Tout d’abord, n’oublions pas que nous cherchons un repère pour nous guider face à l’ambivalence du mimétisme ; or, le partage 50/50 ne nous guide en rien face à l’ambivalence : il en est au contraire l’incarnation ! A l’instar du célèbre verre, à la fois à moitié plein et à moitié vide.

La deuxième raison est plus décisive encore, et c’est à nouveau René Girard qui nous la souffle : en divisant par deux, nous créons deux entités strictement identiques, c’est-à-dire que nous installons immédiatement les conditions du conflit mimétique. La division à la proportion du Nombre d’or donne deux entités ; la petite ne peut être tenue pour négligeable par rapport à l’autre ; mais une hiérarchie est installée, nous évitons ainsi la « crise du degree », dont René Girard a commenté les effets dévastateurs.

Retenons donc la proportion du Nombre d’or comme repère dans la dialectique du proche et du lointain, c’est-à-dire de l’ambivalence du mimétisme.

Mais alors, que peut bien signifier d’imiter quelqu’un à 61,8% ? de partager 61,8% des opinions d’un autre ? d’adopter comme raison de vivre 61,8% de celle de son modèle ?

Il n’existe aucune procédure pour répondre à de telles questions (aucune « recette » si vous préférez un terme moins technocratique). Le recours à nos facultés inventives est inévitable. A chacun de voir s’il préfère une existence créatrice ou procédurale…